Grafas

Grafas – figūra, sudaryta iš taškų (vadinamų viršūnėmis) ir iš atkarpų, jungiančių kai kurias šių viršūnių. Jungiančios atkarpos gali būti tiesios arba kreivos, jos vadinamos grafo briaunomis. Frafas G susideda iš dviejų aibių: V_i- viršūnių aibė, B_i- briaunų aibė.G=({V_i},{B_i}). 1 pav.

Dar apie grafus:
• Dvi viršūnės yra kaimyninės, jei jos sujungtos briauna B_k=(V_i, V_j). A kaimyninės viršūnės yra B ir E.
• Kelias tai tarp viršūnių esanti seka briaunų, pradedant viena viršūne ir baigiant kita viršūne. Jei kelias per kiekvieną jam priklausančią viršūnę praeina tik po vieną kartą, tada jis vadinamas paprastu keliu.
• Ciklas yra paprastas kelias, kuris prasideda ir baigiasi toje pačioje viršūnėje.
• Jungus grafas – jei egzistuoja kelias tarp bet kurių viršūnių porų.
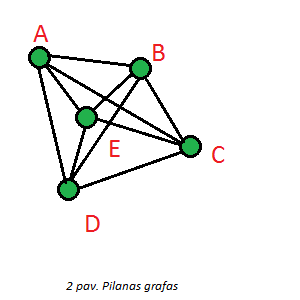
• Pilnas grafas – jei yra briauna tarp kiekvienos viršūnių poros.
• Grafo briaunoms galima suteikti skaitines reikšmes (svorius), toks grafas vadinamas grafu su svoriais.
• Grafai, kurių briaunos neturi krypties, t.y. briauna galima keliauti bet kuria kryptimi, neorientuotais grafais
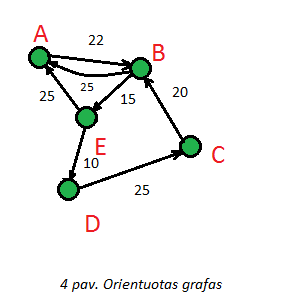
• Briaunai galima suteikti kryptį, tokia briauna vadinama lanku. Grafas, kurio briaunos turi kryptis, vadinamas orientuotu (kryptiniu) grafu. Orientuotas grafas yra sudarytas iš viršūnių aibės ir lankų aibės.